#c

栈(Stack)

数据结构基础

#c
@鞠大龙
魅客科创中心

CONTENTS

目录

1. 栈的基本概念

1.1 栈的定义

  • 栈(Stack)的定义：
    • 栈是一种线性数据结构
    • 只允许在一端（栈顶）进行插入和删除操作
    • 遵循 后进先出(LIFO, Last In First Out) 原则
    • 可以类比为一摞盘子或一叠书
  • 栈的特点：
    • 操作受限的线性表
    • 插入和删除操作都在同一端进行
    • 最后插入的元素最先被删除
    • 只能访问栈顶元素，无法直接访问栈内其他元素

1.2 LIFO原理

  • 后进先出(LIFO)原理：
    • 最后放入栈中的元素，会最先被取出
    • 最先放入栈中的元素，会最后被取出
    • 类似于日常生活中的"叠盘子"场景
  • LIFO与FIFO的区别：
    • LIFO(Last In First Out)：栈的特性
    • FIFO(First In First Out)：队列的特性
    • 两者是相反的操作原则

1.3 栈的特性

栈的基本特性：

  1. 有序性：
    • 元素在栈中的存储是有序的
    • 但只能按照特定顺序访问（后进先出）
  2. 可逆性：
    • 入栈操作和出栈操作互为逆操作
    • 一系列入栈操作后，相反顺序的出栈操作可以恢复原始状态
  3. 受限访问：
    • 只能访问栈顶元素
    • 要访问栈中间元素，必须先弹出上面的所有元素
  4. 动态大小：
    • 栈的大小可以动态变化
    • 但在某些实现中可能有容量限制

2. 栈的基本操作

2.1 栈的基本操作概述

栈支持的主要操作：

  • push：将元素压入栈顶
  • pop：移除栈顶元素
  • top：查看栈顶元素但不移除
  • empty：检查栈是否为空
  • size：获取栈中元素个数

2.2 Push操作

  • Push操作：
    • 将一个元素添加到栈顶
    • 时间复杂度：
  • 实现步骤：
    1. 检查栈是否已满（数组实现时）
    2. 将元素放入栈顶位置
    3. 栈顶指针加1
  • 示例代码：
void push(int value) {
    if (top >= capacity - 1) {
        cout << "Stack Overflow" << endl;
        return;
    }
    arr[++top] = value;
}

Push操作示意图：

#c

注意事项：

  • 数组实现时需要检查栈是否已满
  • 链表实现时通常不需要检查容量
  • STL实现时会自动处理内存分配

2.3 Pop操作

  • Pop操作：
    • 移除栈顶元素
    • 时间复杂度：
  • 实现步骤：
    1. 检查栈是否为空
    2. 获取栈顶元素
    3. 栈顶指针减1
    4. 返回之前的栈顶元素
  • 示例代码：
void pop() {
    if (top < 0) {
        cout << "Stack Underflow" << endl;
        return;
    }
    top--;
}

Pop操作示意图：

#c

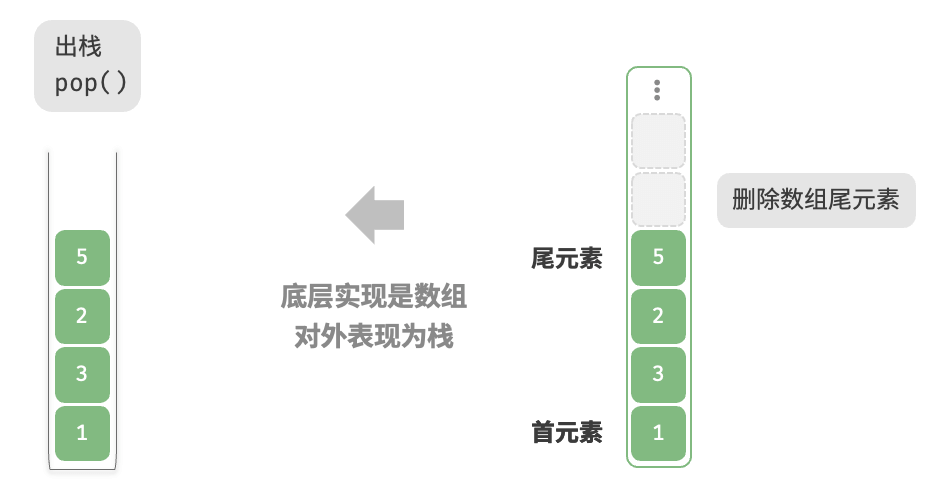
注意事项：

  • 必须检查栈是否为空
  • 弹出元素后，该位置的内存仍然保留原值
  • 但该位置逻辑上已不属于栈
  • 连续pop操作会按照LIFO顺序删除元素

2.4 Top操作

Top操作：

  • 返回栈顶元素但不移除
  • 时间复杂度：
    实现步骤：
  1. 检查栈是否为空
  2. 返回栈顶元素的值
    示例代码：
int top() {
    if (top < 0) {
        cout << "Stack is Empty" << endl;
        return -1;
    }
    return arr[top];
}

注意事项：

  • 与pop操作不同，top操作不会修改栈的状态
  • 常用于需要查看栈顶元素但不想移除它的场景
  • 在某些实现中也称为peek操作

2.5 其他操作

  • Empty操作：
    • 检查栈是否为空
    • 时间复杂度：
bool isEmpty() {
    return (top < 0);
}
  • Size操作：
    • 返回栈中元素的数量
    • 时间复杂度：
int size() {
    return top + 1;
}
  • isFull操作（数组实现时）：
    • 检查栈是否已满
    • 时间复杂度：
bool isFull() {
    return (top == capacity - 1);
}
  • Clear操作：
    • 清空栈中所有元素
    • 时间复杂度：
void clear() {
    top = -1;
}

3. 栈的实现方式

3.1 数组实现栈

  • 数组实现栈的基本思路：
    • 使用一维数组存储栈元素
    • 使用一个变量跟踪栈顶位置
    • 入栈和出栈操作通过移动栈顶指针实现
  • 优点：
    • 实现简单直观
    • 随机访问速度快
    • 内存布局连续，缓存友好
  • 缺点：
    • 需要预先分配空间
    • 可能会导致空间浪费
    • 栈满时需要扩容（动态数组）

完整实现代码：

class ArrayStack {
private:
    int* arr;
    int top;
    int capacity;

public:
    ArrayStack(int size) {
        arr = new int[size];
        capacity = size;
        top = -1;
    }
    
    ~ArrayStack() {
        delete[] arr;
    }
    
    void push(int x) {
        if (isFull()) {
            cout << "Stack Overflow" << endl;
            return;
        }
        arr[++top] = x;
    }
    
    int pop() {
        if (isEmpty()) {
            cout << "Stack Underflow" << endl;
            return -1;
        }
        return arr[top--];
    }
    
    int peek() {
        if (isEmpty()) return -1;
        return arr[top];
    }
    
    bool isEmpty() { return top == -1; }
    bool isFull() { return top == capacity - 1; }
    int size() { return top + 1; }
};

3.2 链表实现栈

  • 链表实现栈的基本思路：
    • 使用单链表存储栈元素
    • 将链表的头部作为栈顶
    • 入栈和出栈操作在链表头部进行
  • 优点：
    • 动态分配内存，不需要预先确定大小
    • 不存在栈满的问题
    • 空间利用率高
  • 缺点：
    • 需要额外的内存存储指针
    • 操作稍微复杂
    • 不支持随机访问

完整实现代码：

class LinkedListStack {
private:
    struct Node {
        int data;
        Node* next;
        Node(int d) : data(d), next(nullptr) {}
    };
    
    Node* top;
    int stackSize;

public:
    LinkedListStack() : top(nullptr), stackSize(0) {}
    
    ~LinkedListStack() {
        while (!isEmpty()) {
            pop();
        }
    }
    
    void push(int x) {
        Node* newNode = new Node(x);
        newNode->next = top;
        top = newNode;
        stackSize++;
    }
    
    int pop() {
        if (isEmpty()) {
            cout << "Stack Underflow" << endl;
            return -1;
        }
        int value = top->data;
        Node* temp = top;
        top = top->next;
        delete temp;
        stackSize--;
        return value;
    }
    
    int peek() {
        if (isEmpty()) return -1;
        return top->data;
    }
    
    bool isEmpty() { return top == nullptr; }
    int size() { return stackSize; }
};

3.3 STL stack使用

  • C++ STL stack：
    • C++标准库提供的栈容器适配器
    • 默认基于deque实现，也可基于vector或list
    • 提供完整的栈操作接口
  • STL stack的主要操作：
    • push()：将元素压入栈顶
    • pop()：移除栈顶元素
    • top()：返回栈顶元素
    • empty()：检查栈是否为空
    • size()：返回栈中元素个数
  • 注意事项：
    • pop()不返回被删除的元素
    • 使用top()前应确保栈非空
    • 可以指定底层容器：
      stack<int, vector<int>> s;
stack<int, list<int>> s;
    • STL stack是容器适配器，不支持迭代器

3.3 STL stack使用(续)

#include <iostream>
#include <stack>
usng namespace std;

int main() {
    stack<int> s;

    // 向栈中添加元素
    s.push(10);
    s.push(20);
    s.push(30);

    // 打印栈顶元素
    cout << "Top element is: " << s.top() << endl; // 输出: Top element is: 30

    // 移除栈顶元素
    s.pop();
    cout << "After popping, top element is: " << s.top() << endl; // 输出: After popping, top element is: 20

    // 检查栈是否为空
    if (!s.empty()) {
        cout << "Stack is not empty." << endl; // 输出: Stack is not empty.
    }

    // 打印栈的大小
    cout << "Size of stack: " << s.size() << endl; // 输出: Size of stack: 2

    // 继续移除元素
    s.pop();
    s.pop();

    // 检查栈是否为空
    if (s.empty()) {
        cout << "Stack is empty." << endl; // 输出: Stack is empty.
    }

    return 0;
}

3.4 栈的实现比较

特性 数组实现 链表实现 STL stack
内存分配 静态/预分配 动态分配 动态分配
空间效率 可能浪费 高效 高效
时间效率 操作O(1) 操作O(1) 操作O(1)
实现复杂度 简单 中等 最简单(直接使用)
扩展性 有限 良好 良好
缓存友好性 高 低 中等
适用场景 大小可预测 大小不可预测 一般用途
溢出风险 有栈溢出风险 无栈溢出风险 无栈溢出风险

选择建议：

  • 对于大小已知且较小的栈，可以使用数组实现
  • 对于大小不确定或可能很大的栈，使用链表实现
  • 对于一般应用，推荐使用STL stack

4. 栈的应用场景

4.1 函数调用

  • 函数调用栈：
    • 存储函数调用的上下文信息
    • 管理函数的局部变量
    • 处理函数的返回
  • 工作原理：
    1. 调用函数时压栈：
      • 返回地址
      • 参数
      • 局部变量
    2. 函数返回时出栈：
      • 恢复调用点
      • 清理局部变量
      • 获取返回值

示例代码：

void function3() {
    int x = 3;
    // 函数3的栈帧在最顶部
}

void function2() {
    int y = 2;
    function3();  // 调用function3
    // function3返回后继续执行
}

void function1() {
    int z = 1;
    function2();  // 调用function2
    // function2返回后继续执行
}

int main() {
    function1();  // 调用function1
    return 0;
}

4.2 表达式求值

  • 表达式求值应用：
    • 计算算术表达式
    • 处理运算符优先级
    • 转换表达式格式（中缀转后缀）
  • 实现思路：
    1. 使用两个栈：
      • 运算符栈
      • 操作数栈
    2. 遍历表达式：
      • 数字直接入操作数栈
      • 运算符按优先级处理
    3. 计算结果：
      • 弹出运算符和操作数
      • 执行运算
      • 结果压回操作数栈

示例代码：

int evaluateExpression(string expr) {
    stack<int> values;
    stack<char> ops;
    
    for (int i = 0; i < expr.length(); i++) {
        if (isdigit(expr[i])) {
            int val = 0;
            while (i < expr.length() && 
                   isdigit(expr[i])) {
                val = val * 10 + (expr[i] - '0');
                i++;
            }
            i--;
            values.push(val);
        }
        else if (expr[i] == '(') {
            ops.push(expr[i]);
        }
        else if (expr[i] == ')') {
            while (!ops.empty() && 
                   ops.top() != '(') {
                int val2 = values.top(); 
                values.pop();
                int val1 = values.top(); 
                values.pop();
                char op = ops.top(); 
                ops.pop();
                values.push(applyOp(val1, val2, op));
            }
            ops.pop(); // 弹出'('
        }
        else if (expr[i] == '+' || 
                 expr[i] == '-' || 
                 expr[i] == '*' || 
                 expr[i] == '/') {
            while (!ops.empty() && 
                   precedence(ops.top()) >= 
                   precedence(expr[i])) {
                int val2 = values.top(); 
                values.pop();
                int val1 = values.top(); 
                values.pop();
                char op = ops.top(); 
                ops.pop();
                values.push(applyOp(val1, val2, op));
            }
            ops.push(expr[i]);
        }
    }
    
    while (!ops.empty()) {
        int val2 = values.top(); 
        values.pop();
        int val1 = values.top(); 
        values.pop();
        char op = ops.top(); 
        ops.pop();
        values.push(applyOp(val1, val2, op));
    }
    
    return values.top();
}

4.3 括号匹配

  • 括号匹配问题：
    • 检查括号是否正确配对
    • 支持多种类型的括号
    • 常见于代码编辑器和编译器
  • 实现思路：
    1. 遇到左括号时入栈
    2. 遇到右括号时：
      • 检查栈是否为空
      • 检查栈顶括号是否匹配
      • 匹配则出栈
    3. 最后检查栈是否为空

示例代码：

bool isValid(string s) {
    stack<char> st;
    
    for (char c : s) {
        if (c == '(' || c == '{' || c == '[') {
            st.push(c);
        }
        else {
            if (st.empty()) return false;
            
            if (c == ')' && st.top() != '(') 
                return false;
            if (c == '}' && st.top() != '{') 
                return false;
            if (c == ']' && st.top() != '[') 
                return false;
            
            st.pop();
        }
    }
    
    return st.empty();
}

4.4 其他应用场景

  1. 深度优先搜索(DFS)：
    • 使用栈存储待访问的节点
    • 实现回溯功能
    • 图和树的遍历
  2. 撤销操作：
    • 存储操作历史
    • 实现Undo/Redo功能
    • 文本编辑器的实现
  3. 浏览器历史：
    • 前进/后退功能
    • 网页访问记录
    • 会话管理
  1. 内存管理：
    • 函数调用栈
    • 程序执行上下文
    • 异常处理
  2. 编译器实现：
    • 语法分析
    • 表达式求值
    • 代码生成

5. 经典例题

5.1 括号匹配问题

POJ 1426. Find The Multiple

问题描述：
给定一个括号序列，包含小括号'('和')'，判断该序列是否合法。合法的定义是每个左括号都有一个对应的右括号，且括号序列正确嵌套。

解题思路：

  1. 使用栈存储左括号
  2. 遇到右括号时检查栈顶是否匹配
  3. 最后检查栈是否为空

完整代码：

#include <iostream>
#include <stack>
#include <string>
using namespace std;

bool isValid(string s) {
    stack<char> st;
    
    for (char c : s) {
        if (c == '(') {
            st.push(c);
        } else if (c == ')') {
            if (st.empty()) return false;
            st.pop();
        }
    }
    
    return st.empty();
}

int main() {
    string s;
    while (cin >> s) {
        if (isValid(s)) {
            cout << "YES" << endl;
        } else {
            cout << "NO" << endl;
        }
    }
    return 0;
}

5.2 中缀表达式转后缀

HDU 1237. 简单计算器

问题描述：
实现一个简单的计算器，支持加减乘除四种运算，没有括号。

解题思路：

  1. 使用栈将中缀表达式转换为后缀表达式
  2. 使用栈计算后缀表达式的值
  3. 处理运算符优先级
  4. 处理连续的数字和运算符

示例：

输入：3 + 5 * 2
输出：13

5.2 代码示例

实现代码：

#include <bits/stdc++.h>
using namespace std;

int calculate(string s) {
    stack<int> nums;
    stack<char> ops;
    
    stringstream ss(s);
    int num;
    char op;
    
    // 读取第一个数字
    ss >> num;
    nums.push(num);
    
    while (ss >> op) {
        if (op == '0') break;
        
        // 读取下一个数字
        ss >> num;
        
        // 根据运算符优先级处理
        if (op == '+' || op == '-') {
            while (!ops.empty()) {
                char top_op = ops.top();
                ops.pop();
                
                int b = nums.top(); nums.pop();
                int a = nums.top(); nums.pop();
                
                if (top_op == '+') nums.push(a + b);
                else if (top_op == '-') nums.push(a - b);
                else if (top_op == '*') nums.push(a * b);
                else if (top_op == '/') nums.push(a / b);
            }
            ops.push(op);
        } else { // * 或 /
            while (!ops.empty() && (ops.top() == '*' || ops.top() == '/')) {
                char top_op = ops.top();
                ops.pop();
                
                int b = nums.top(); nums.pop();
                int a = nums.top(); nums.pop();
                
                if (top_op == '*') nums.push(a * b);
                else nums.push(a / b);
            }
            ops.push(op);
        }
        
        nums.push(num);
    }
    
    // 处理剩余的运算符
    while (!ops.empty()) {
        char top_op = ops.top();
        ops.pop();
        
        int b = nums.top(); nums.pop();
        int a = nums.top(); nums.pop();
        
        if (top_op == '+') nums.push(a + b);
        else if (top_op == '-') nums.push(a - b);
        else if (top_op == '*') nums.push(a * b);
        else if (top_op == '/') nums.push(a / b);
    }
    
    return nums.top();
}

int main() {
    string s;
    while (getline(cin, s) && s != "0") {
        cout << calculate(s) << endl;
    }
    return 0;
}

5.3 直方图最大矩形

POJ 2559. 直方图中最大的矩形

问题描述：
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。

解题思路：

  1. 使用单调栈
  2. 栈中存储柱子的索引
  3. 当前柱子高度小于栈顶时计算面积
  4. 维护递增的高度序列

实现代码：

#include <iostream>
#include <stack>
#include <vector>
#include <algorithm>
using namespace std;

typedef long long LL;

LL largestRectangleArea(vector<int>& heights) {
    stack<int> st;
    heights.push_back(0); // 添加哨兵
    LL maxArea = 0;
    
    for (int i = 0; i < heights.size(); i++) {
        while (!st.empty() && heights[st.top()] > heights[i]) {
            int height = heights[st.top()];
            st.pop();
            int width = st.empty() ? i : i - st.top() - 1;
            maxArea = max(maxArea, (LL)height * width);
        }
        st.push(i);
    }
    
    heights.pop_back(); // 移除哨兵
    return maxArea;
}

int main() {
    int n;
    while (cin >> n && n != 0) {
        vector<int> heights(n);
        for (int i = 0; i < n; i++) {
            cin >> heights[i];
        }
        cout << largestRectangleArea(heights) << endl;
    }
    return 0;
}

复杂度分析：

  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

5.4 单调栈应用

CSES 1645. 最近的较小值

问题描述：
给定一个包含n个整数的数组。对于每个位置，找出位于其左侧的第一个比当前值小的元素的位置。如果不存在这样的元素，输出0。

解题思路：

  1. 使用单调栈维护左侧的元素
  2. 对于每个新元素：
    • 弹出栈中所有大于等于当前元素的值
    • 栈顶即为左侧第一个较小值
  3. 维护单调递增栈

实现代码：

#include <iostream>
#include <stack>
#include <vector>
using namespace std;

int main() {
    int n;
    cin >> n;
    vector<int> arr(n);
    for (int i = 0; i < n; i++) {
        cin >> arr[i];
    }
    
    // 使用pair存储值和索引
    stack<pair<int,int>> st;
    vector<int> result(n);
    
    for (int i = 0; i < n; i++) {
        // 弹出所有大于等于当前值的元素
        while (!st.empty() && st.top().first >= arr[i]) {
            st.pop();
        }
        
        // 如果栈为空，说明左侧没有更小的值
        if (st.empty()) {
            result[i] = 0;
        } else {
            // 栈顶元素即为左侧第一个较小值
            result[i] = st.top().second + 1;
        }
        
        // 将当前元素入栈
        st.push({arr[i], i});
    }
    
    // 输出结果
    for (int i = 0; i < n; i++) {
        cout << result[i] << " ";
    }
    cout << endl;
    
    return 0;
}

示例：

输入:
8
2 5 1 4 8 3 2 5
输出:
0 1 0 3 4 3 3 7

6. 优化技巧

6. 优化技巧

  • 空间优化：
    • 使用动态数组实现栈，根据需要调整容量
    • 使用内存池减少频繁的内存分配和释放
    • 考虑使用压缩技术存储特定类型的数据
  • 时间优化：
    • 避免不必要的复制操作
    • 使用移动语义(C++11)提高效率
    • 预分配足够的空间避免频繁扩容
  • 常见陷阱：
    • 栈为空时进行pop或top操作
    • 忽略栈满的情况(数组实现)
    • 内存泄漏(链表实现)
    • 递归调用过深导致栈溢出
  • 特殊优化：
    • 双栈技术：使用两个栈实现队列
    • 最小栈：O(1)时间获取栈中最小元素
    • 栈的批量操作：减少函数调用开销

7. 总结

7. 总结

核心要点：

  • 栈的基本概念
    • 后进先出(LIFO)原则
    • 只能在栈顶进行操作
    • 受限的线性数据结构
  • 栈的基本操作
    • push：入栈
    • pop：出栈
    • top：查看栈顶
    • empty：检查是否为空
    • size：获取元素个数
  • 栈的实现方式
    • 数组实现
    • 链表实现
    • STL stack

应用场景：

  • 函数调用管理
  • 表达式求值
  • 括号匹配
  • 深度优先搜索
  • 撤销操作
  • 浏览器历史
  • 编译器实现

经典例题：

  • 有效的括号
  • 中缀表达式转后缀
  • 直方图最大矩形
  • 每日温度问题

8. 练习题目

8.1 初级练习题

  1. [HDU 1062] Text Reverse

    • 难度：★★☆☆☆
    • 描述：将一行文本中的每个单词反转，但保持单词的顺序不变
    • 思路：使用栈存储每个单词的字符，然后弹出实现反转

  2. [POJ 1363] Rails

    • 难度：★★☆☆☆
    • 描述：判断给定的出栈序列是否可能通过特定的入栈序列得到
    • 思路：模拟入栈出栈过程，检查是否能得到目标序列

  3. [CSES 1619] Restaurant Customers

    • 难度：★★☆☆☆
    • 描述：给定顾客的到达和离开时间，计算餐厅同时最多有多少顾客
    • 思路：使用栈或优先队列处理时间点，模拟顾客进出

8.2 中级练习题

  1. [POJ 3250] Bad Hair Day

    • 难度：★★★☆☆
    • 描述：计算每头牛能看到右边多少头牛的背部
    • 思路：使用单调栈维护可见的牛的高度

  2. [HDU 4699] Editor

    • 难度：★★★☆☆
    • 描述：实现一个简单的文本编辑器，支持插入、删除和撤销操作
    • 思路：使用栈存储操作历史，实现撤销功能

  3. [CSES 1142] Advertisement

    • 难度：★★★☆☆
    • 描述：在广告牌上找出最大的矩形面积
    • 思路：类似直方图最大矩形问题，使用单调栈解决

8.3 高级练习题

  1. [POJ 2082] Terrible Sets

    • 难度：★★★★☆
    • 描述：给定一系列矩形的宽度和高度，求能形成的最大矩形面积
    • 思路：使用单调栈，类似直方图最大矩形问题

  2. [CSES 1076] Sliding Median

    • 难度：★★★★☆
    • 描述：计算滑动窗口中的中位数
    • 思路：使用两个栈或优先队列维护窗口元素

  3. [CSP-S 2019] 括号序列

    • 难度：★★★★☆
    • 描述：给定一个括号序列，求最少添加多少个括号能使序列合法
    • 思路：使用栈模拟括号匹配过程，计算需要添加的括号数量

8.4 综合应用题

  1. [USACO 2016 Feb Gold] Circular Barn

    • 难度：★★★★★
    • 描述：优化奶牛进入圆形牛棚的路径，最小化总行走距离
    • 思路：使用单调队列或栈优化动态规划过程

  2. [POJ 1028] Web Navigation

    • 难度：★★★★★
    • 描述：实现网页浏览器的前进、后退和访问新页面功能
    • 思路：使用两个栈分别存储历史和前进记录

  3. [CSP-J 2022] 解密

    • 难度：★★★★★
    • 描述：解密一段加密文本，需要按特定规则处理嵌套的加密结构
    • 思路：使用栈处理嵌套结构，递归解析加密内容
栈(Stack)

#c

演讲者备注不会在演示模式中显示给观众，仅供演讲者参考。 每个关键页面都添加了备注，帮助演讲者更好地讲解内容。

封面页： - 欢迎学生，简要介绍本次课程的主题和目标 - 强调栈在数据结构和算法中的重要性 - 本讲义将从基本概念到实际应用，系统讲解栈的原理和应用

目录页： - 简要介绍讲义结构 - 栈的基本概念、操作、实现、应用、例题等

转场页： - 介绍栈的基本概念 - 引入LIFO原理

栈的定义： - 基础知识介绍 - 与其他数据结构的区别

转场页： - 介绍栈的基本操作 - 引入push、pop等核心操作

转场页： - 介绍栈的不同实现方式 - 数组实现和链表实现的比较

转场页： - 介绍栈的实际应用场景 - 展示栈在编程中的重要性

转场页： - 介绍栈的经典应用例题 - 通过实例加深理解

转场页： - 介绍栈实现的优化技巧 - 提高栈操作的效率

转场页： - 总结栈的核心概念和应用

转场页： - 栈的练习题目

练习题目部分结束，这些题目涵盖了栈的各个难度和应用场景。 鼓励学生尝试解决这些问题，加深对栈的理解。